Tutorial 3: A Zero-Dimensional Energy Balance Model#
Week 1, Day 5, Introduction to Climate Modeling
Content creators: Jenna Pearson, Brian E. J. Rose
Content reviewers: Mujeeb Abdulfatai, Nkongho Ayuketang Arreyndip, Jeffrey N. A. Aryee, Younkap Nina Duplex, Zahra Khodakaramimaghsoud, Will Gregory, Paul Heubel, Zahra Khodakaramimaghsoud, Peter Ohue, Agustina Pesce, Abel Shibu, Derick Temfack, Yunlong Xu, Peizhen Yang, Chi Zhang, Ohad Zivan
Content editors: Paul Heubel, Brodie Pearson, Abigail Bodner, Ohad Zivan, Chi Zhang
Production editors: Wesley Banfield, Paul Heubel, Jenna Pearson, Konstantine Tsafatinos, Chi Zhang, Ohad Zivan
Our 2024 Sponsors: CMIP, NFDI4Earth
Tutorial Objectives#
Estimated timing of tutorial: 30 minutes
In this tutorial students will learn about the heat capacity of the atmosphere and oceans, how this related to temperature changes over time, and set up their first climate model.
By the end of this tutorial students will be able to:
Calculate the heat capacity of the ocean and atmosphere.
Create and run a time-dependent model of the change in global mean surface temperature in response to energy imbalances.
Describe the influence of transmissivity and albedo on the equilibrium temperature from this model.
Bonus: Understand what equilibrium climate sensitivity is and how to find it using the model.
This tutorial is based on content from The Climate Laboratory by Brian E. J. Rose.
Setup#
# imports
import numpy as np # used for algebra and array operations
import matplotlib.pyplot as plt # used for plotting
Install and import feedback gadget#
Show code cell source
# @title Install and import feedback gadget
!pip3 install vibecheck datatops --quiet
from vibecheck import DatatopsContentReviewContainer
def content_review(notebook_section: str):
return DatatopsContentReviewContainer(
"", # No text prompt
notebook_section,
{
"url": "https://pmyvdlilci.execute-api.us-east-1.amazonaws.com/klab",
"name": "comptools_4clim",
"user_key": "l5jpxuee",
},
).render()
feedback_prefix = "W1D5_T3"
[notice] A new release of pip is available: 24.2 -> 24.3.1
[notice] To update, run: pip install --upgrade pip
Figure settings#
Show code cell source
# @title Figure settings
import ipywidgets as widgets # interactive display
%config InlineBackend.figure_format = 'retina'
plt.style.use(
"https://raw.githubusercontent.com/neuromatch/climate-course-content/main/cma.mplstyle"
)
Video 1: A Zero-Dimensional Energy Balance Model#
Submit your feedback#
Show code cell source
# @title Submit your feedback
content_review(f"{feedback_prefix}_A_Zero_Dimensional_Energy_Balance_Model_Video")
If you want to download the slides: https://osf.io/download/5mgns/
Submit your feedback#
Show code cell source
# @title Submit your feedback
content_review(f"{feedback_prefix}_A_Zero_Dimensional_Energy_Balance_Model_Slides")
Section 1: Building the Model#
Section 1.1: Moving Forward in Time#
One of the crucial things missing from the simple model we have looked at so far is its ability to change with time.
As the composition of the atmosphere (among other things) changes, in response, so does the energy balance and global mean surface temperature. This is shown by the thick black lines in the figure below, where the time series of observed global mean surface air temperature change from the 1850-1900 reference period is plotted. Figures like this are called ‘hockey stick’ figures due to their shape: a relatively stable period followed by a steep increase.
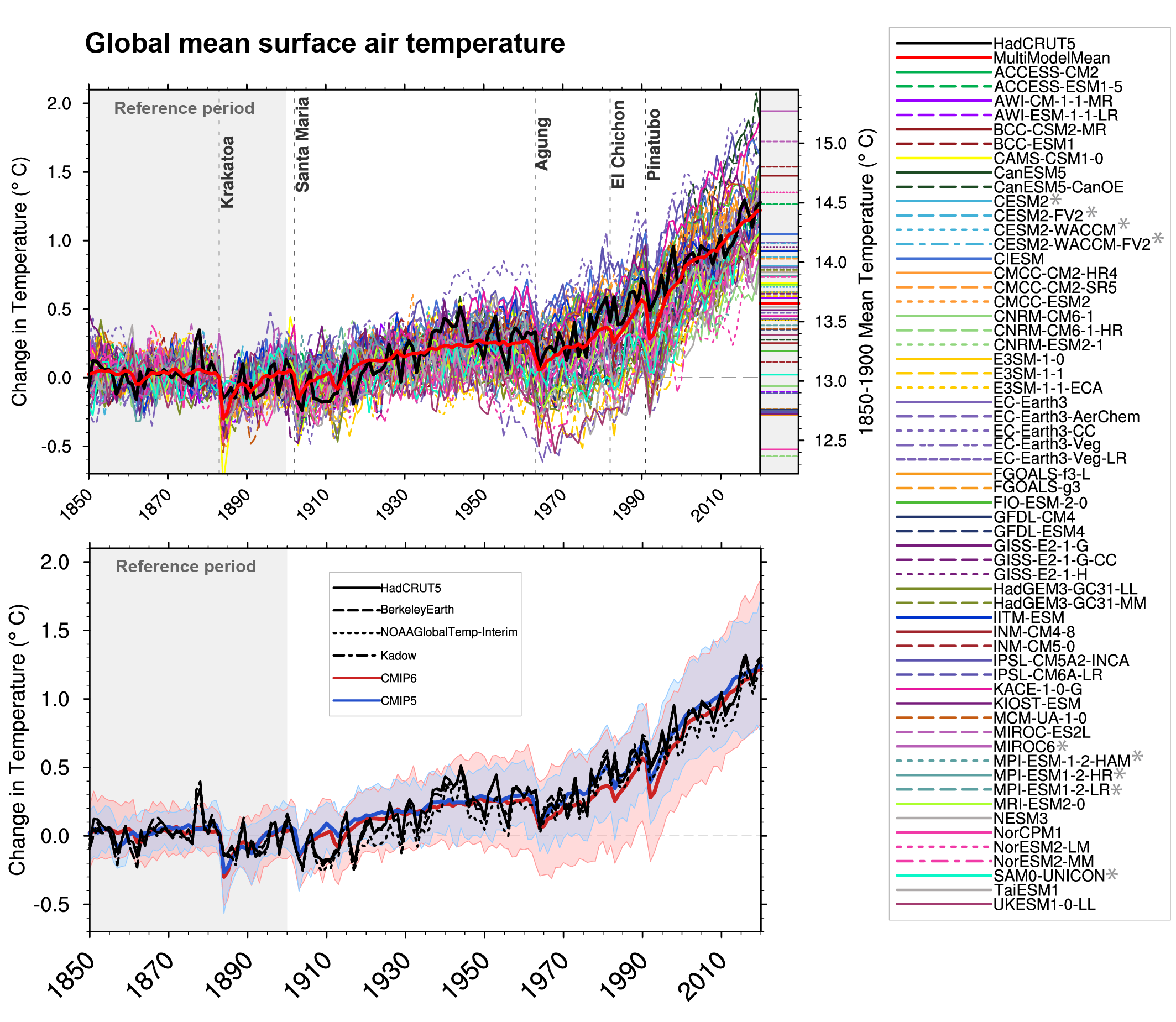Figure 3.4 | Observed and simulated time series of the anomalies in annual and global mean surface air temperature (GSAT). All anomalies are differences from the 1850–1900 time mean of each individual time series. The reference period 1850–1900 is indicated by grey shading. (a) Single simulations from CMIP6 models (thin lines) and the multi-model mean (thick red line). Observational data (thick black lines) are from the Met Office Hadley Centre/Climatic Research Unit dataset (HadCRUT5), and are blended surface temperature (2 m air temperature over land and sea surface temperature over the ocean). All models have been subsampled using the HadCRUT5 observational data mask. Vertical lines indicate large historical volcanic eruptions. CMIP6 models which are marked with an asterisk are either tuned to reproduce observed warming directly, or indirectly by tuning equilibrium climate sensitivity. Inset: GSAT for each model over the reference period, not masked to any observations. (b) Multi-model means of CMIP5 (blue line) and CMIP6 (red line) ensembles and associated 5th to 95th percentile ranges (shaded regions). Observational data are HadCRUT5, Berkeley Earth, National Oceanic and Atmospheric Administration NOAAGlobalTemp-Interim and Kadow et al. (2020). Masking was done as in (a). CMIP6 historical simulations were extended with SSP2-4.5 simulations for the period 2015–2020 and CMIP5 simulations were extended with RCP4.5 simulations for the period 2006–2020. All available ensemble members were used (see Section 3.2). The multi-model means and percentiles were calculated solely from simulations available for the whole time span (1850–2020). The figure is updated from Bock et al. (2020), their Figures 1 and 2. CC BY 4.0 https://creativecommons.org/licenses/by/4.0/. Further details on data sources and processing are available in the chapter data table (Table 3.SM.1). (Credit: IPCC Report AR6)
In order to incorporate time-dependent behavior into our model, we need to include a mathematical representation of how the change in energy relates to a change in temperature over time.
We can represent the change in temperature over time as the net heat input or loss from radiation (\(ASR-OLR\)) multiplied by the heat capacity of the Earth system.
As we learned in Day 2 of this week, the heat capacity of a medium is its ability to increase in temperature given an input of heat. Not all components of the Earth system (for example land, ocean, atmosphere) have the same heat capacity.
Mathematically, the rate of change of global mean surface temperature (\(T\)) over time is given as
where \(C\) is the heat capacity of the Earth system. Note here that when \(ASR > OLR\), then the system is gaining heat. Conversely when \(ASR < OLR\), then the system is losing heat over time.
To calculate the heat capacity for the Earth system, we will assume that it is a combination of atmosphere and ocean only, that is \(C = C_{\text{oc}} + C_{\text{atmo}}\).
Generally, the heat capacity of a medium is the specific heat of that medium times the total mass.
For the atmosphere, we have \(C_{\text{atm}} = c_{\text{atm}} \cdot \frac{W_{\text{atm}}}{g} \) where \(c_{\text{atm}}\) is the specific heat of the atmosphere, \(W_{\text{atm}}\) is the weight of a column of air, and \(g\) is the acceleration due to gravity.
For the ocean we have \(C_{\text{oc}} = c_{\text{oc}} \cdot \rho_{\text{oc}} \cdot d_{\text{oc}}\) where \(c_{\text{oc}}\) is the specific heat of the ocean, \(\rho_{\text{oc}}\) is the density of seawater, and \(d_{\text{oc}}\) is a representative depth of the ocean.
We will use these definitions to find the heat capacities of the atmosphere and ocean and to refresh what we learned on Day 2.
# heat capacity of the ocean
c_oc = 3850 # specific heat of seawater in J/kg/K
rho_oc = 1025 # average density of seawater in kg/m3
d_oc = 70 # depth of water in m (here representative of the mixed layer)
C_oc = c_oc * rho_oc * d_oc # heat capacity of the ocean
# heat capacity of the atmosphere
c_atm = 1004 # specific heat of the atmosphere at constant pressure in J/kg/K
W_atm = 100000 # weight (pressure) of atmospheric column in Pa
g = 9.81 # acceleration due to gravity in m/s^2
C_atm = c_atm * (W_atm / g) # heat capacity of the atmosphere
# total heat capacity
C = C_oc + C_atm
# print results
print(f'Ocean Heat Capacity: {C_oc:.2f} J m^-2 K^-1')
print(f'Atmosphere Heat Capacity: {C_atm:.2f} J m^-2 K^-1')
print(f'Total Heat Capacity: {C:.2f} J m^-2 K^-1')
Ocean Heat Capacity: 276237500.00 J m^-2 K^-1
Atmosphere Heat Capacity: 10234454.64 J m^-2 K^-1
Total Heat Capacity: 286471954.64 J m^-2 K^-1
Coding Exercises 1.1#
Calculate the depth of the ocean needed for the ocean to have the same heat capacity as the atmosphere.
# heat capacity of the atmosphere
c_atm = 1004 # specific heat of the atmosphere at constant pressure in J/kg/K
W_atm = 100000 # weight (pressure) of atmospheric column in Pa
g = 9.81 # height of atmosphere in m (representative of )
C_atm = c_atm * (W_atm / g) # heat capacity of the atmosphere
# find the depth of the ocean for equivalent atmospheric heat capacity
c_oc = 3850 # specific heat of seawater in J/kg/K
rho_oc = 1025 # average density of seawater in kg/m3
d_oc = ...
d_oc
Ellipsis
Submit your feedback#
Show code cell source
# @title Submit your feedback
content_review(f"{feedback_prefix}_Coding_Exercises_1_1")
Section 1.2: The Numerical Model#
Knowing the heat capacity, and the descriptions of \(OLR\) and \(ASR\) from previous tutorials, we can write the equation
First note that
So the equation for our model can be written
Numerically, we can use this equation to compute the global mean surface temperature after a small interval of time by adding on the amount of energy gained or lost multiplied by the time interval itself.
The particular method of numerically defining the time and temperature intervals (changes) is called discretization, and the way we have chosen to do this is called the Forward Euler method. The exact details of this method are beyond the scope of this tutorial, and we will use the method without further elaboration.
The Forward Euler method assumes we can use \(\text{change in }T = T_{n+1} - T_{n}\) and \(\text{change in t} = t_{n+1} - t_{n}\) where \(t\) is time. Thus, if we know the time interval and the current temperature \(\left(T_n\right)\), we can predict the temperature at the end of our time interval, \(\left(T_{n+1}\right)\).
# define the time interval, currently one year expressed in seconds
dt = 60.0 * 60.0 * 24.0 * 365.0
# define albedo
alpha = 0.2941 # unitless number between 0 and 1 (calculated previously from observations in tutorial 2)
# define transmissivity (calculated previously from observations in tutorial 1)
tau = 0.6127 # unitless number between 0 and 1
# define a function for absorbed shortwave radiation (ASR)
def ASR(alpha, Q):
return (1 - alpha) * Q
# define a function for outgoing longwave radiation (OLR)
def OLR(tau, T):
# define the Stefan-Boltzmann Constant, noting we are using 'e' for scientific notation
sigma = 5.67e-8 # W m^-2 K^-4
return tau * sigma * T**4
# create a function to find the new temperature based on the previous using Euler's method.
def step_forward(T, alpha, tau, dt):
# define the observed insolation based on observations from the IPCC AR6 Figure 7.2
Q = 340 # W m^-2
# find the new temperature using forward Euler method
T_new = T + dt / C * (ASR(alpha, Q) - OLR(tau, T))
return T_new
We can now use a loop to apply this function many times over by specifying an initial temperature and a time interval. Note we will be using lists to do so.
# define the number of timesteps (currently years) to run the model
numtsteps = 15
# for converting number of seconds in a year
sec_2_yr = 3.154e7
# set the intial temperature (initial condition)
T_series = [288]
# set the initial time to 0
t_series = [0]
# run the model
for n in range(numtsteps):
# calculate and append the time since running the model, dependent on dt and the numtsteps
t_series.append((n + 1) * dt / sec_2_yr)
# calculate and append the new temperature using our pre-defined function
T_series.append(step_forward(T_series[n], alpha=alpha, tau=tau, dt=dt))
# display the temeprature time series
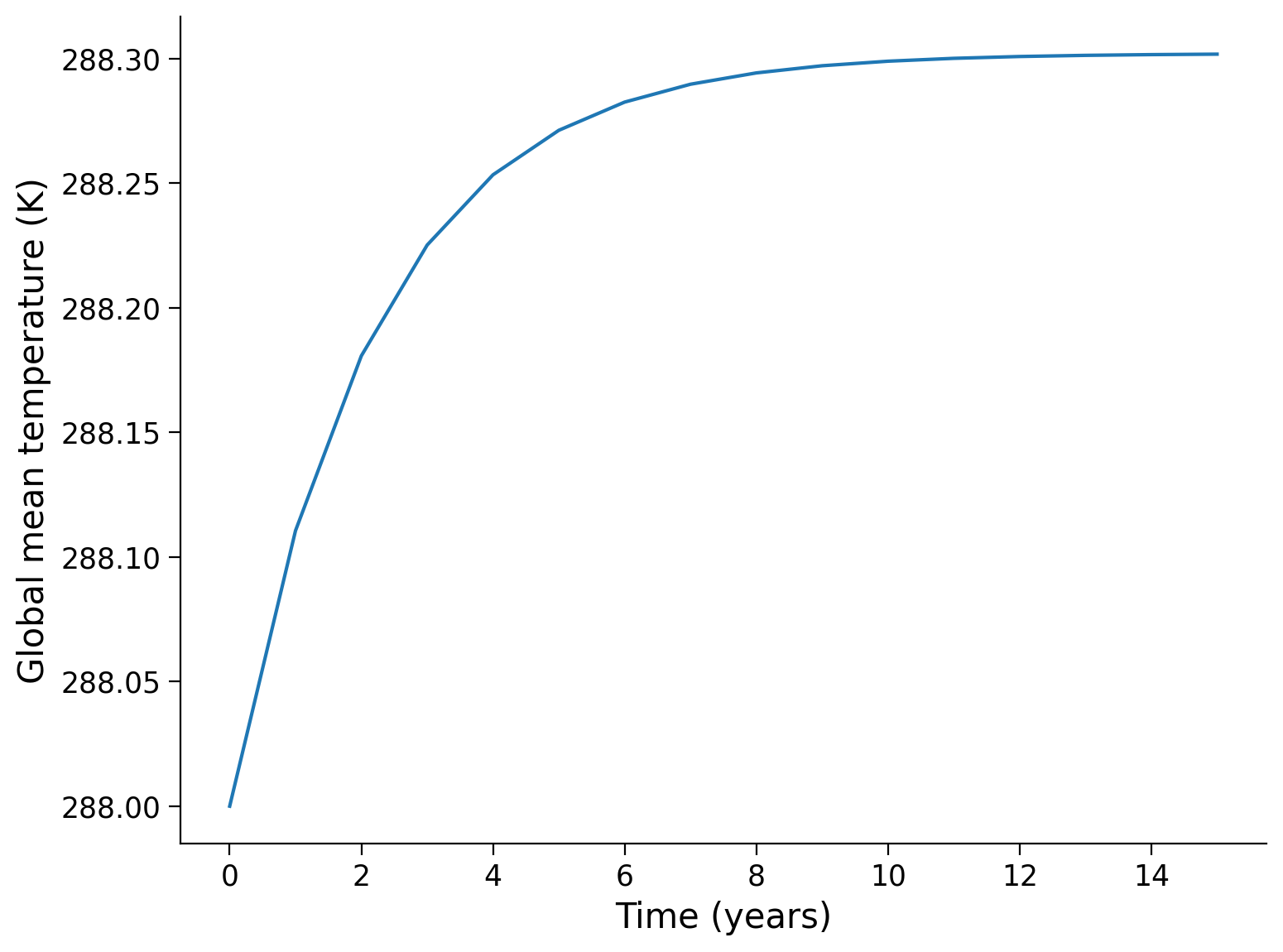
print(T_series)
[288, 288.1105634820389, 288.18070153127155, 288.22517079984357, 288.25335571129256, 288.2712155880614, 288.2825312527962, 288.28970000469195, 288.29424133262887, 288.2971181140696, 288.29894041951593, 288.300094747791, 288.30082594344617, 288.3012891080957, 288.3015824915692, 288.30176832972967]
# display the time series
print(t_series)
[0, 0.9998731769181991, 1.9997463538363982, 2.999619530754597, 3.9994927076727964, 4.999365884590995, 5.999239061509194, 6.999112238427394, 7.998985415345593, 8.998858592263792, 9.99873176918199, 10.99860494610019, 11.998478123018389, 12.998351299936589, 13.998224476854787, 14.998097653772987]
# plot the results
fig, ax = plt.subplots()
ax.plot(t_series, T_series)
ax.set_xlabel("Time (years)")
ax.set_ylabel("Global mean temperature (K)")
Text(0, 0.5, 'Global mean temperature (K)')
Questions 1.2#
Do you think the time step (interval) we have used will affect the solution? If so, how?
Submit your feedback#
Show code cell source
# @title Submit your feedback
content_review(f"{feedback_prefix}_Questions_1_2")
Coding Exercise 1.2#
Using a for loop, run the model for 15 years with three different intervals (\(dt\)) of a half year, 1 year, and 5 years and plot the results. Note you will have to change the number of timesteps used when changing
dtso that the model runs for the same amount of time. Plot your results on the same figure.
# one year expressed in seconds
one_yr = 60.0 * 60.0 * 24.0 * 365.0
# legend labels
labels = ["dt = half-year", "dt = one year", "dt = five years"]
# define the number of timesteps (years) to run the model
numtsteps = np.array([10, 5, 1]) * 3
# for converting the number of seconds in a year
sec_2_yr = 3.154e7
fig, ax = plt.subplots()
# loop through each choice of time step
for dd, dt_2 in enumerate([one_yr * 0.5, one_yr, one_yr * 5]):
# set the intial temperature (initial condition)
...
# set the initial time to 0
...
# run the model
for n in range(numtsteps[dd]):
# calculate and append the time since running the model, dependent on dt and the numtsteps
...
# calculate and append the new temperature using our pre-defined function step_forward()
...
ax.plot(t_series, T_series, label=labels[dd])
ax.set_xlabel("Time (years)")
ax.set_ylabel("Global mean temperature (K)")
ax.legend()
<matplotlib.legend.Legend at 0x7fbca9b51df0>
Example output:
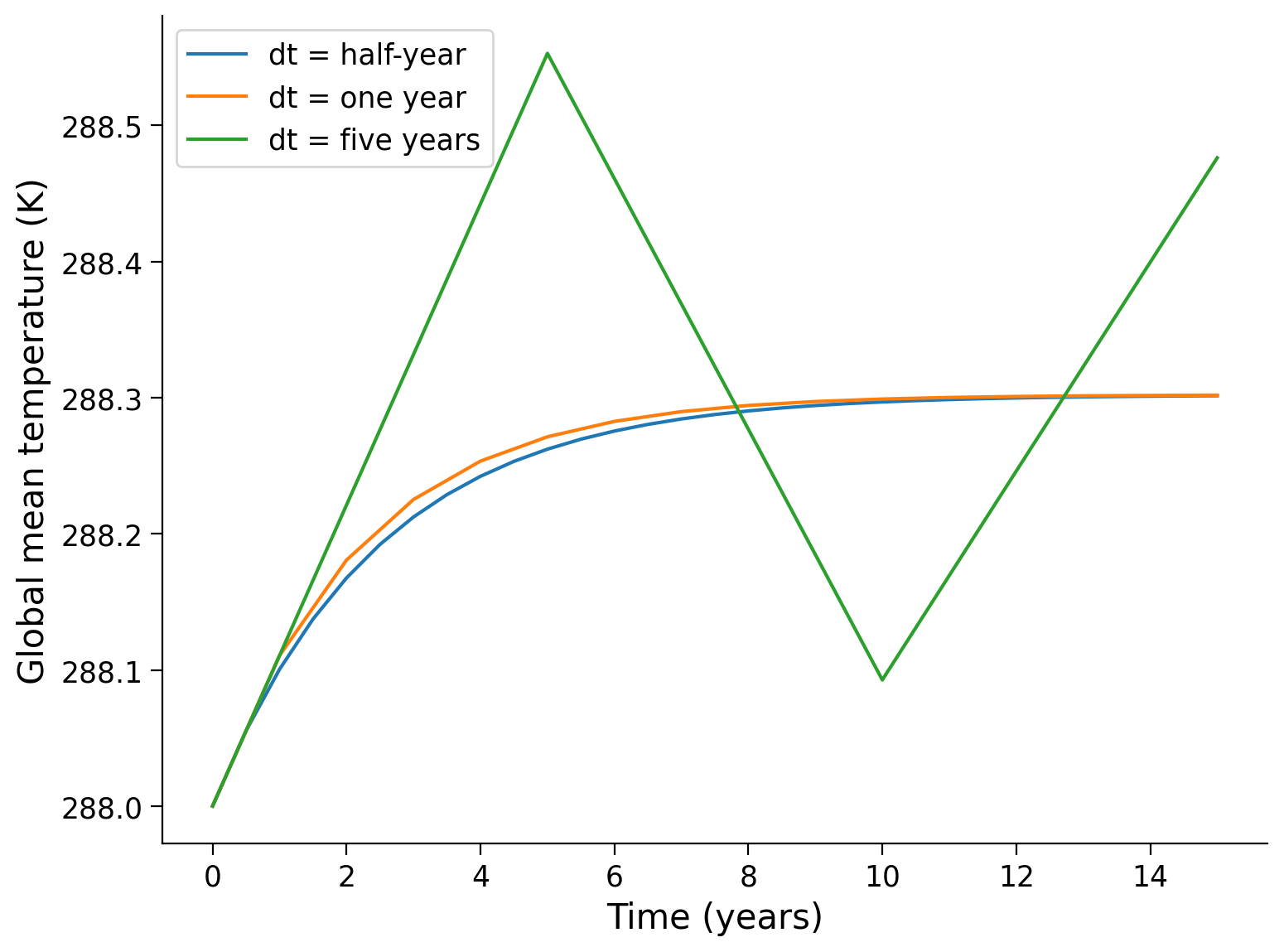
Submit your feedback#
Show code cell source
# @title Submit your feedback
content_review(f"{feedback_prefix}_Coding_Exercises_1_2")
Section 2: Revisiting the Climate Change Scenario from Tutorial 2#
Section 2.1: Enhanced Greenhouse Effect#
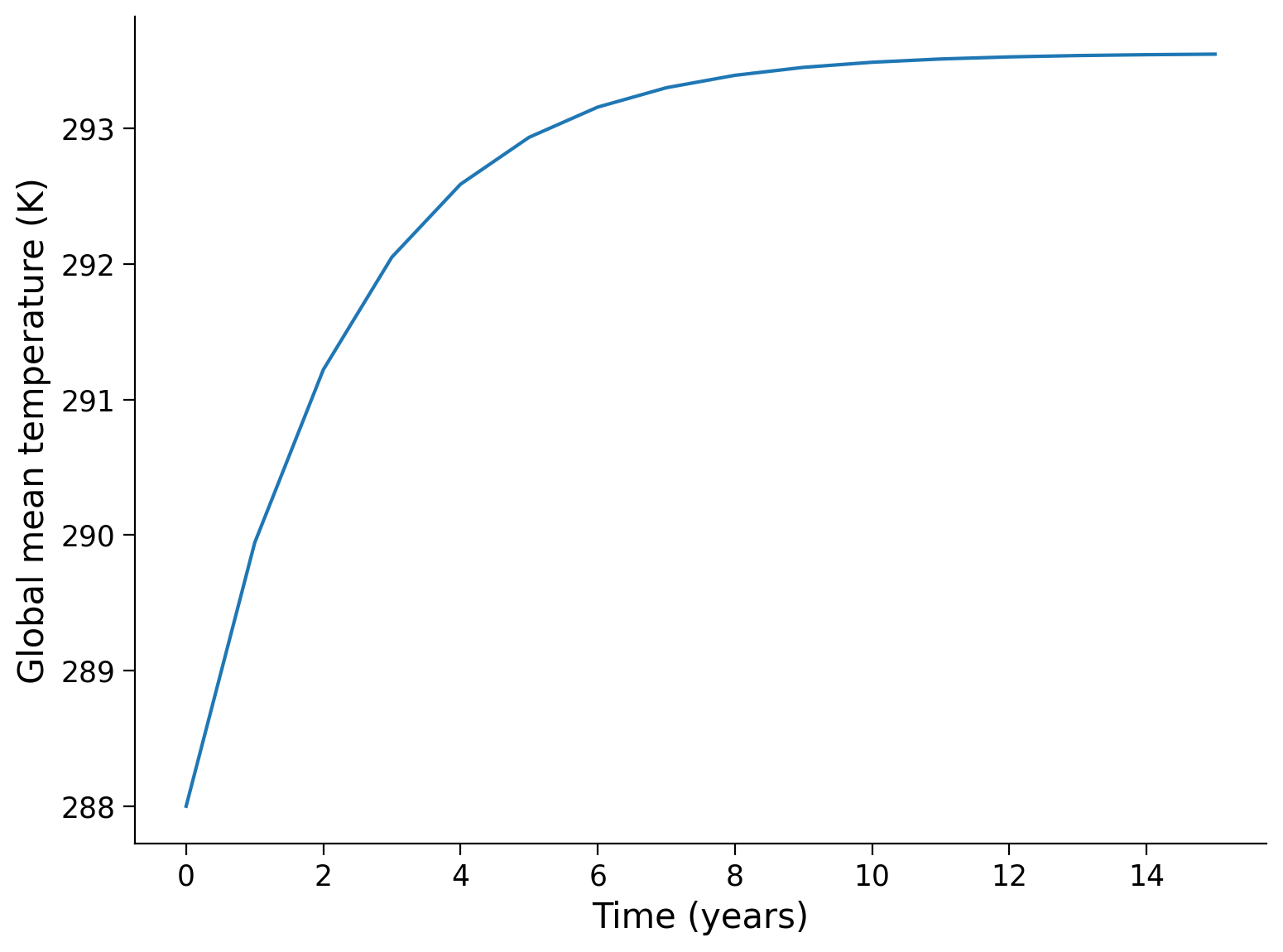
In Tutorial 2 we looked at how changing the transmissivity \(\left(\tau\right)\) affected the equilibrium temperature \(T_{\text{eq}}\). Now we can use our time-dependent model to investigate this in more depth. Reuse the model, this time setting \(\tau = 0.57\).
# define transmissivity (calculated previously from observations)
tau_2 = 0.57 # unitless number between 0 and 1
# define the number of timesteps (currently years) to run the model
numtsteps = 15
# set the intial temperature (initial condition)
T_series = [288]
# set the initial time to 0
t_series = [0]
# run the model
for n in range(numtsteps):
# calculate and append the time since running the model, dependent on dt and the numtsteps
t_series.append((n + 1) * dt / sec_2_yr)
# calculate and append the new temperature using our pre-defined function
T_series.append(step_forward(T_series[n], alpha=alpha, tau=tau_2, dt=dt))
fig, ax = plt.subplots()
ax.plot(t_series, T_series)
ax.set_xlabel("Time (years)")
ax.set_ylabel("Global mean temperature (K)")
Text(0, 0.5, 'Global mean temperature (K)')
Bonus Coding Exercise: Equilibrium Climate Sensitivity#
Here we define the equilibrium climate sensitivity as the long-term global warming (equilibrium temperature increase) caused by a doubling of carbon dioxide above its pre-industrial concentration. The impact of a doubling of carbon dioxide on these energy flows is measured by a radiative forcing. Here a positive radiation forcing leads to warming, and a negative radiative forcing leads to cooling.
The equilibrium climate sensitivity depends on a number of things, including physics and feedbacks of the model used. In the following exercise, you will calculate the equilibrium climate sensitivity of our model.
Write a function called
step_forward()as from above, and then create another function that adds in a radiative forcing to the difference between \(ASR\) and \(OLR\) and call itstep_forward_forced(). Make sure both functions output the energy balance of the model. Consistent with the IPCC AR6, use an effective radiative forcing of 3.93 W m\(^{-2}\), where effective means the climate system, but not the surface temperature, has been allowed to adjust.
# define your functions and constants
# define albedo
alpha = 0.2941 # unitless number between 0 and 1 (calculated previously from observations in tutorial 2)
# define transmissivity (calculated previously from observations in tutorial 1)
tau = 0.6127 # unitless number between 0 and 1
# effective radiative forcing for a doubling of CO2
F = 3.93 # W/m^2
# define the time interval, one year expressed in seconds
dt = 60.0 * 60.0 * 24.0 * 365.0
# for converting number of seconds in a year
sec_2_yr = 3.154e7
# define a function for absorbed shortwave radiation (ASR)
def ASR(alpha, Q):
return (1 - alpha) * Q
# define a function for outgoing longwave radiation (OLR)
def OLR(tau, T):
# define the Stefan-Boltzmann Constant, noting we are using 'e' for scientific notation
sigma = 5.67e-8 # W m^-2 K^-4
return tau * sigma * T**4
# create a function to find the new temperature based on the previous using Euler's method.
def step_forward(T, alpha, tau, dt):
# define the observed insolation based on observations from the IPCC AR6 Figure 7.2
...
# define the Stefan-Boltzmann Constant, noting we are using 'e' for scientific notation
...
Ftoa = ...
T_new = ...
return ...
# create a function to find the new temperature based on the previous using Euler's method.
def step_forward_forced(T, alpha, tau, dt):
# define the observed insolation based on observations from the IPCC AR6 Figure 7.2
...
# define the Stefan-Boltzmann Constant, noting we are using 'e' for scientific notation
...
Ftoa = ...
T_new = ...
return ...
Submit your feedback#
Show code cell source
# @title Submit your feedback
content_review(f"{feedback_prefix}_Bonus_Coding_Exercises_3_1")
Using an initial temperature of 288 K, run the model to equilibrium. Make sure your model is in equilbrium by checking that the energy balance is near zero.
# run the model to equilibrium without forcing and begining with T(0) = 288K
# define the number of timesteps (years) to run the model
numtsteps = 40
# set the intial temperature (initial condition)
T_series = [288]
# set the initial time to 0
t_series = [0]
# run the model
for n in range(numtsteps):
# calculate and append the time since running the model, dependent on dt and the numtsteps
t_series.append(...)
# calculate and append the new temperature using our pre-defined function and get energy balance
...
T_series.append(...)
print(...)
Ellipsis
Submit your feedback#
Show code cell source
# @title Submit your feedback
content_review(f"{feedback_prefix}_Bonus_Coding_Exercises_3_2")
Run the forced model equilibrium using the unforced equilibrium temperature as your inital condition and the
step_forward_forced()function you wrote above.
# define the number of timesteps (years) to run the model
numtsteps = 40
# set initial condition (temperature) to the equilibrium value from the last run without forcing
T_series_forced = [T_series[-1]]
# set the initial time to 0
t_series_forced = [0]
# run the model
for n in range(numtsteps):
# calculate and append the time since running the model, dependent on dt and the numtsteps
t_series_forced.append(...)
# calculate and append the new temperature using our pre-defined function and get energy balance
...
T_series_forced.append(...)
print(...)
Ellipsis
Submit your feedback#
Show code cell source
# @title Submit your feedback
content_review(f"{feedback_prefix}_Bonus_Coding_Exercises_3_3")
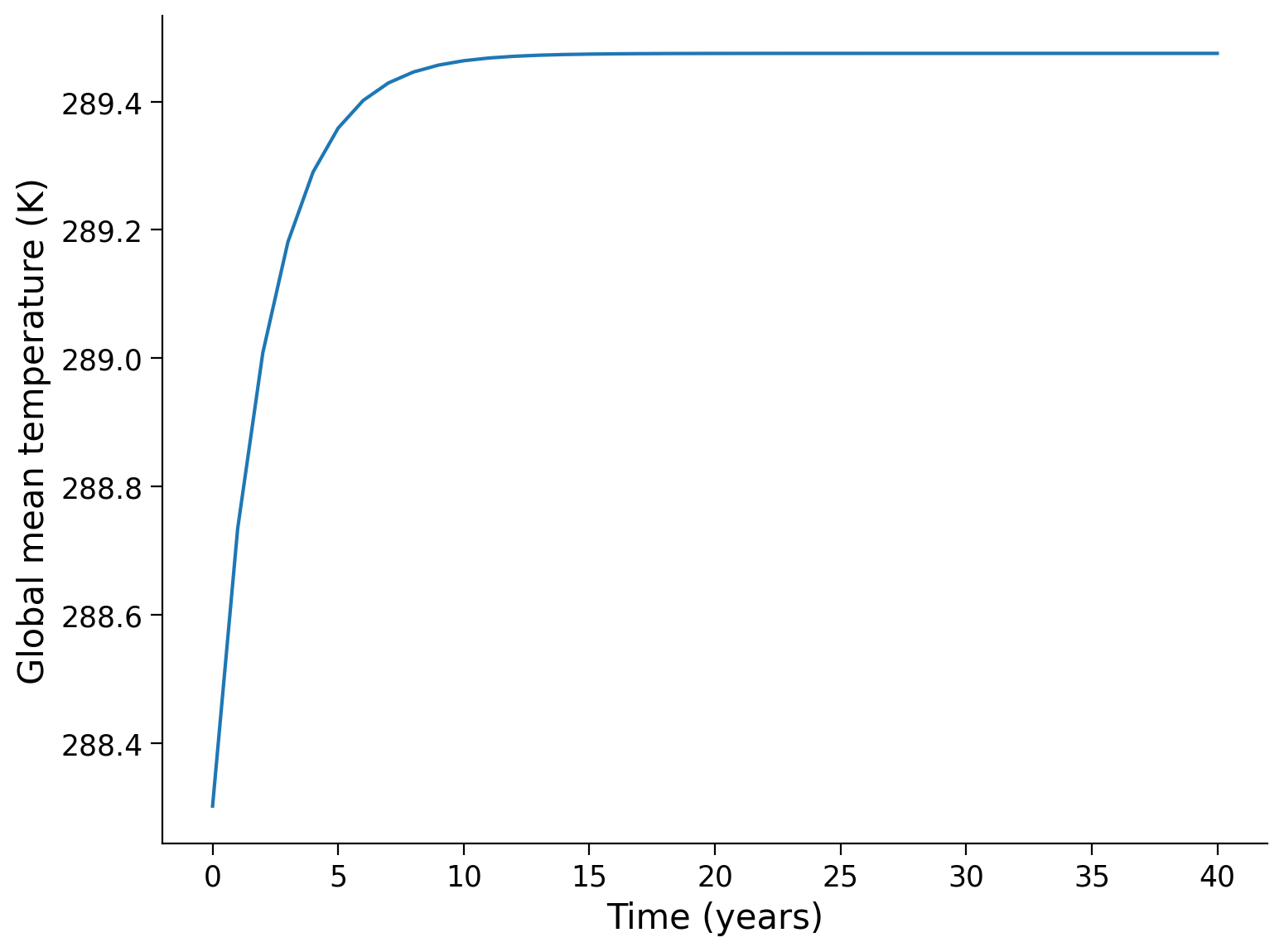
Plot the temperature curve from the forced simulation as a function of time.
# plot the time series
fig, ax = plt.subplots()
_ = ...
ax.set_xlabel("Time (years)")
ax.set_ylabel("Global mean temperature (K)")
Text(0, 0.5, 'Global mean temperature (K)')
Example output:
Submit your feedback#
Show code cell source
# @title Submit your feedback
content_review(f"{feedback_prefix}_Bonus_Coding_Exercises_3_4")
Subtract the intial temperature used for your forced simulation from the final temperature after running to equilibrium to get the equilibrium climate sensitivty.
# calculate equilibrium climate sensitivity
ecs = ...
print("Equilibrium Climate Sensitivity: ", ecs)
Equilibrium Climate Sensitivity: Ellipsis
Submit your feedback#
Show code cell source
# @title Submit your feedback
content_review(f"{feedback_prefix}_Bonus_Coding_Exercises_3_5")
Bonus Questions: Climate Connection#
How does this compare to the IPCC AR6 estimate of equilibrium climate sensitivity of 2-5 K? Is it higher or lower? Note here it is a temperature difference, so the units of C in the report and K found here are interchangeable.
In your own words, describes what this implies with respect to global mean temperatures in our models versus those in used in the IPCC report.
What do you think could be missing in our model?
Submit your feedback#
Show code cell source
# @title Submit your feedback
content_review(f"{feedback_prefix}_Bonus_Questions_3")
Summary#
In this tutorial, you explored the relationship between the heat capacity of the atmosphere and oceans and temperature changes over time. You learned how to calculate the heat capacity of these components and used this knowledge to develop a climate model. This model simulates the change in global mean surface temperature in response to energy imbalances. You explored the effects of transmissivity on the equilibrium temperature and discussed equilibrium climate sensitivity.
Resources#
Useful links: